5 Assumptions of Linear Regression
(BIG MISTAKE) 50% of Data Enthusiasts Overlook This!
When building a linear regression model, it’s tempting to focus solely on achieving a 𝐡𝐢𝐠𝐡 𝐚𝐝𝐣𝐮𝐬𝐭𝐞𝐝 𝐑² and 𝐦𝐢𝐧𝐢𝐦𝐢𝐳𝐢𝐧𝐠 𝐦𝐞𝐚𝐧 𝐬𝐪𝐮𝐚𝐫𝐞𝐝 𝐞𝐫𝐫𝐨𝐫.
However, a model isn’t truly reliable unless it meets key statistical assumptions.
Linear regression relies on several assumptions to ensure the validity and reliability of the model's results.
In this read, let’s explore the 5 Main Assumptions of Linear Regression, in detail.
Before that, if you’re new here Subscribe, as my goal is to simplify Data Science for you. 👇🏻
Now, let’s get started!
Assumptions of Linear Regression:
These assumptions are often asked in Data Science interviews, so understanding them is crucial!
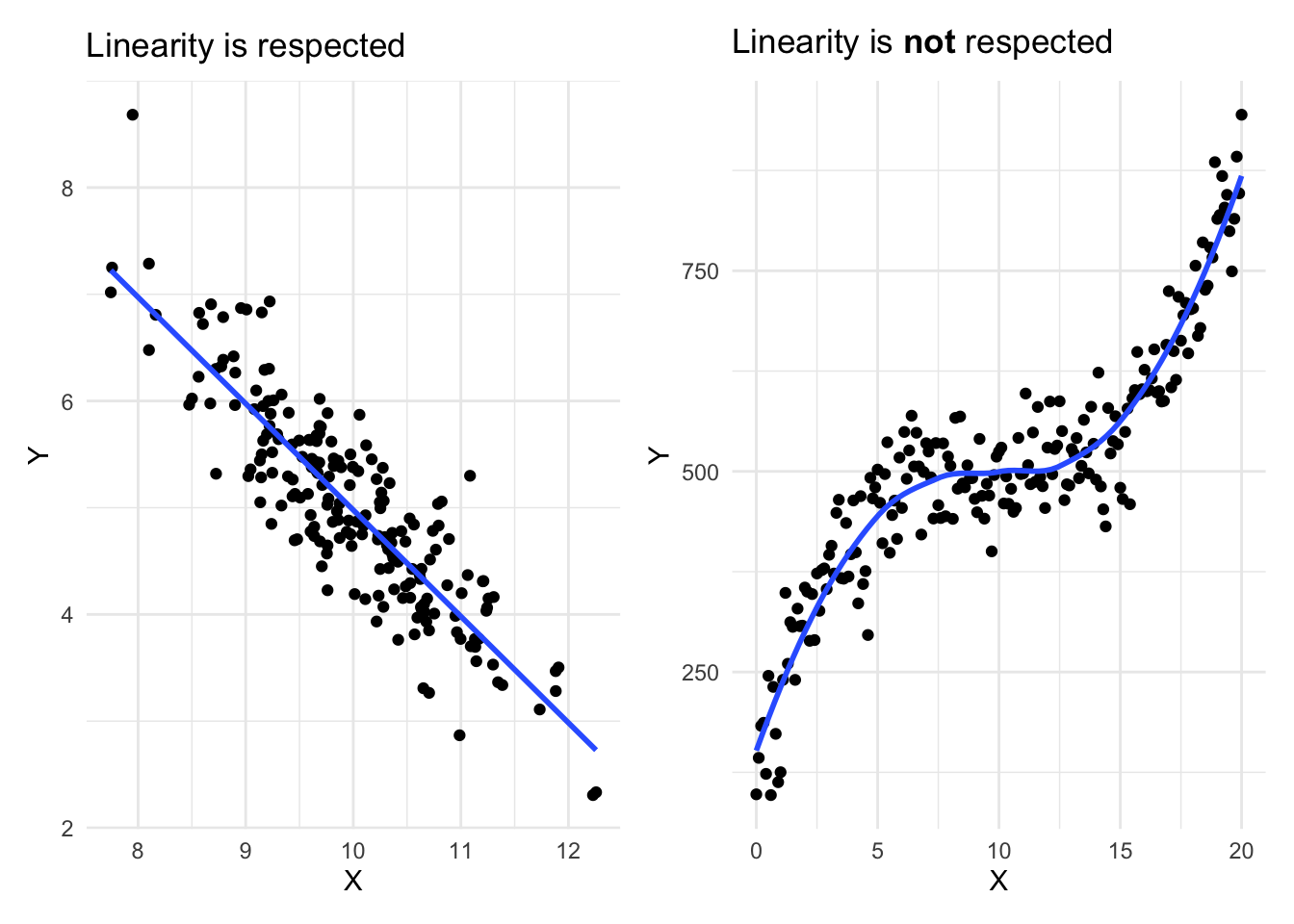
1. Linearity Among Dependent and Independent Variables
For linear regression to work, the relationship between the independent variables (predictors) and the dependent variable (response) should be approximately linear.
This means that the change in the response variable should be proportional to changes in the predictor variables.
How to check?
You can verify this assumption by examining:
Scatter plots: Check if the data points form a straight-line pattern.
Residual plots: Ensure there is no curved pattern.
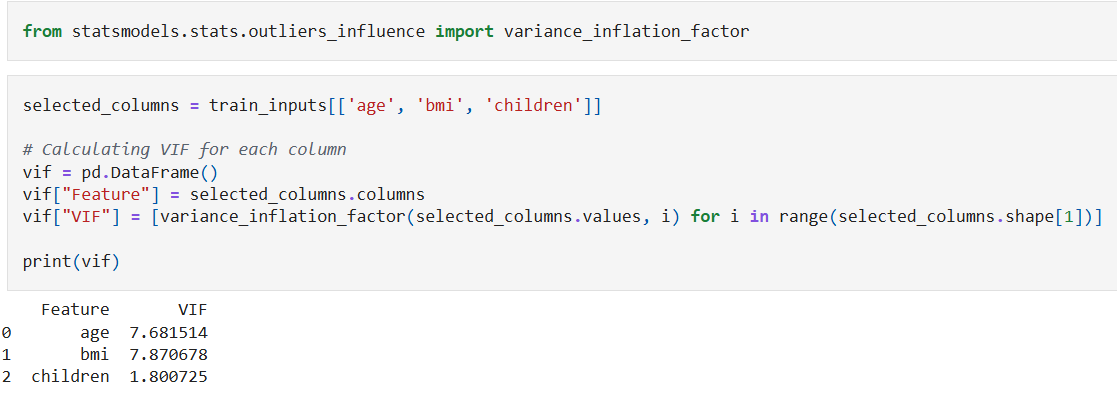
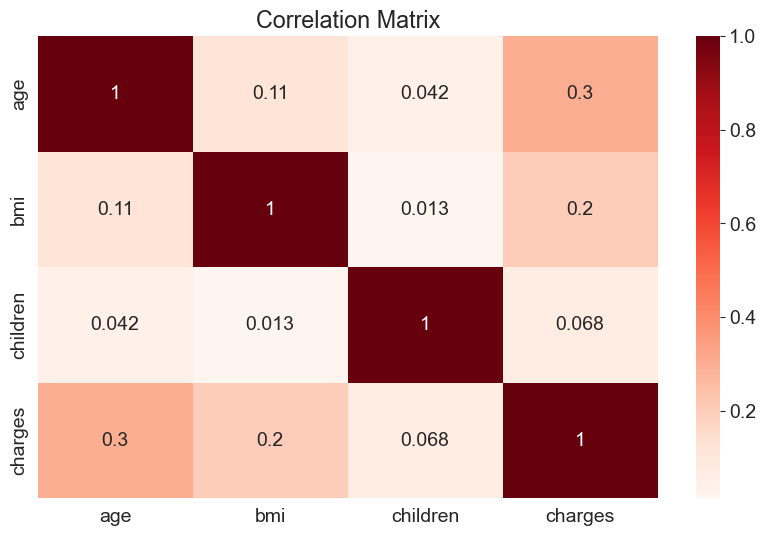
2. No Multicollinearity in the Data
Multicollinearity occurs when one predictor variable is highly correlated with one or more other predictor variables.
This makes it difficult for the model to determine which variable is actually influencing the dependent variable.
How to check?
Variance Inflation Factor (VIF): Measures how much a predictor’s variance is increased by multicollinearity. If VIF > 5 or 10, it indicates high multicollinearity.
Correlation Matrix: Identifies highly correlated predictor variables using the
.corrmethod of a Pandas series.
Important Note: Just because two features are correlated doesn’t mean one causes the other. This is known as Correlation vs Causation Fallacy.
While this may seem obvious, computers can't really differentiate between correlation and causation, why is why human insight is required.
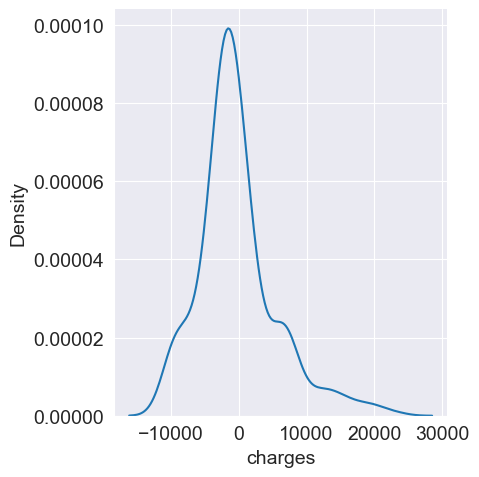
3. Normality of Residuals (or Errors)
The residual (errors) should be normally distributed.
Note: While this is not required for estimating regression coefficiets, it is crucial for hypothesis testing and constructing confidence intervals.
How to check?
Normality of errors can be checked using techniques such as:
Kernel density estimation (KDE): A smoothed representation of the residual distribution.
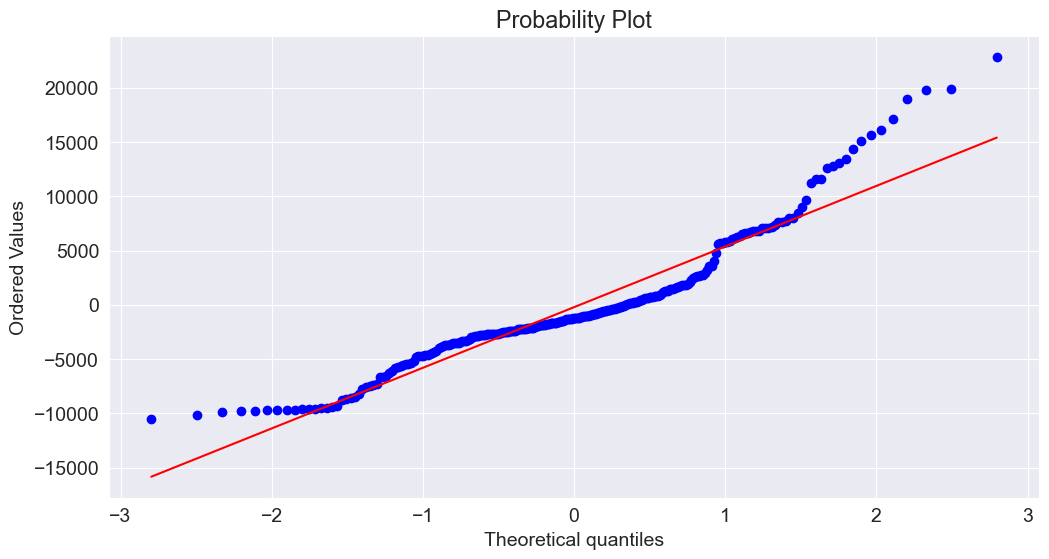
Q-Q Plot: If residuals align with the straight reference line, they are normally distributed.
Shapiro-Wilk Test: A statistical test for normality.
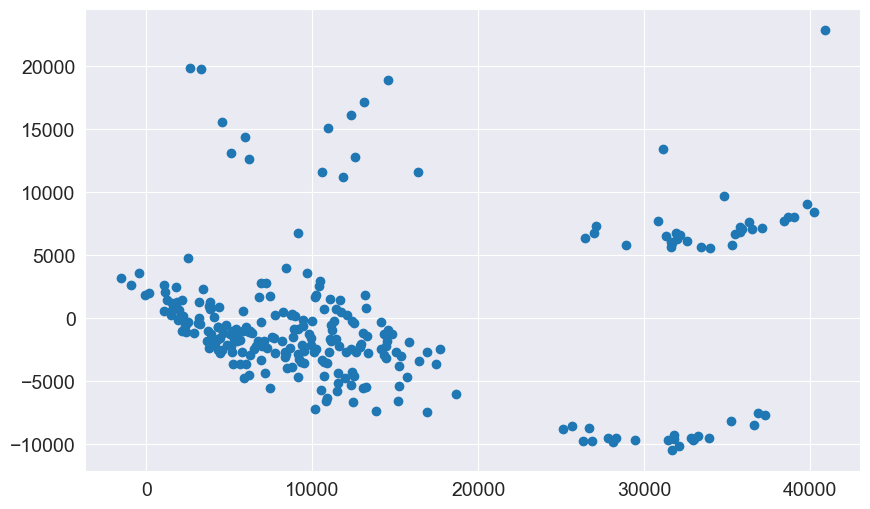
4. Homoscedasticity Among the Data
Homoscedasticity means that the variance of the errors should remains the same for all values of the predictors (independent variables).
If the variance changes (gets bigger or smaller), the assumption is violated, and this is called heteroscedasticity (not preferable).
How to check?
Residual plots: Residuals should be randomly scattered. If there is a funnel shape, it indicates heteroscedasticity.
Since, in above plot the spread of the residuals doesn't have any significant increases or decreases with the test predictor, it suggests homoscedasticity in data.
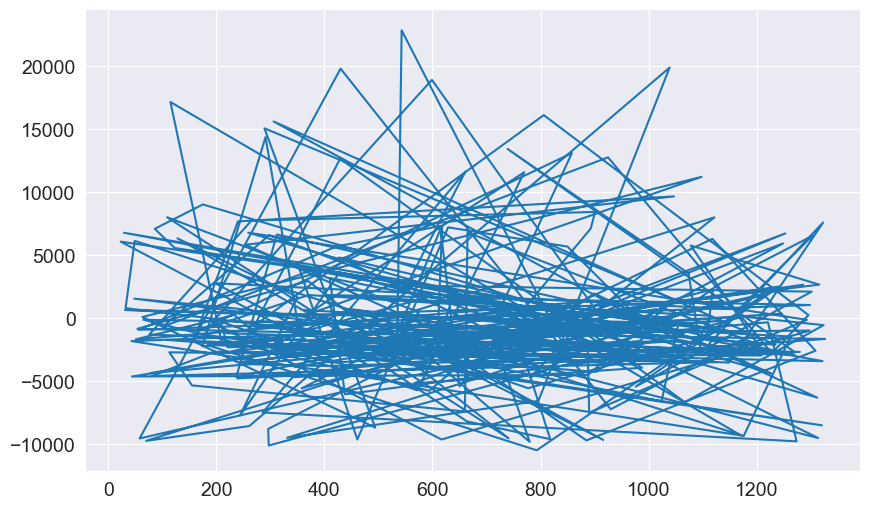
5. No Auto-correlation of Residuals
Auto-correlation happens when the reiduals are related to each other over time.
This usually occurs in time-series data where past values influence future values.
Why is this bad?
If residuals are correlated, the model underestimates the standard error, making predictions unreliable.
How to check?
Durbin-Watson test: A statistical test for detecting autocorrelation.
Residual plot over time: Look for patterns instead of randomness.
Clearly, above plot shows is no pattern or correlation present in the residual points.
If there is no pattern, autocorrelation is not present.
And that’s a wrap, whether you’re a beginner diving into machine learning or an expert, understanding these assumptions will help you build better models.
If you’d like to explore the full implementation, including code and data, then checkout: Github Repository. 👈🏻
Also stay tuned with ME, so you won’t miss out on future updates.
Until next time, happy learning!