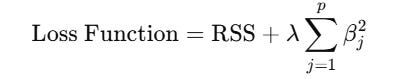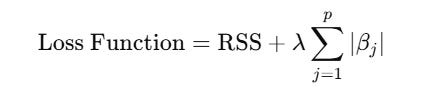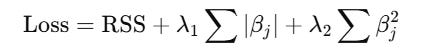Reducing Overfitting Using Regularization
Difference between Ridge and Lasso Regularization
Linear Regression assumes data with no multicollinearity, and no noise.
But real-world datasets, we often have:
Too many features.
Correlated predictors.
Noise, Outliers and much more.
That is why we need regularization.
Let’s break down what it is, different types of regularization techniques, and how to choose between them like a data scientist who knows what they're doing.
And hey — if you’re new here Subscribe, as my goal is to simplify Data Science for you. 👇🏻
Let’s dive in!
Regularization in Machine Learning
It is a statistical method to reduce errors caused by overfitting on training data, by adding a penalty term to the cost function in the model.
This discourages complex models with high coefficients, promoting simpler and more generalizable solutions.
Regularization helps improve a model's performance on unseen data and enhances its overall robustness.
Techniques of Regularization
There are mainly two types of regularization techniques, which are given below:
Ridge Regression (L2 Regularization)
Lasso Regression (L1 Regularization)
each influencing the model's behavior in different ways.
1. Ridge Regression (or L2 Regularization)
Ridge Regression adds a squared penalty to the coefficients:
RSS is the residual sum of squares.
λ (lambda) controls the strength of the penalty.
What It Does:
Keeps all features in the model, but shrinks coefficients toward zero.
Especially helpful when predictors are correlated.
Doesn’t eliminate features—just balances them.
Use Ridge When:
You want to keep all variables, but reduce model complexity.
Multicollinearity is an issue.
Interpretability isn’t your top priority.
2. Lasso Regression (or L1 Regularization)
Lasso uses the absolute value of coefficients:
What It Does:
Shrinks some coefficients exactly to zero.
Performs feature selection automatically.
Helps build sparse models—great for high-dimensional datasets.
Use Lasso When:
You want to select important features and ignore the rest.
Your dataset has many variables, but not all of them matter.
You care about simpler, interpretable models.
Bonus: ElasticNet
Why choose between Ridge and Lasso when you can have both?
ElasticNet combines both L1 and L2 penalties:
Best for:
High-dimensional data.
When predictors are correlated.
Note: Elastic Net seems to perform empirically better which combines both the above methods.
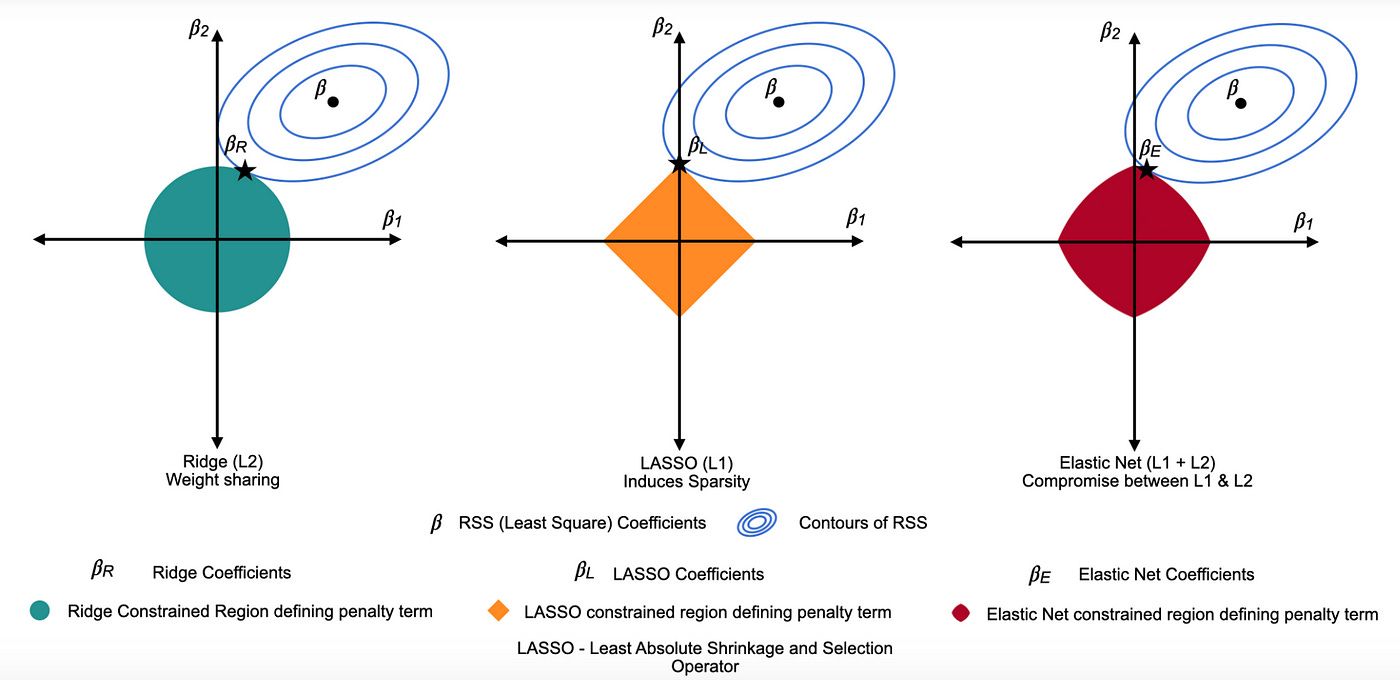
Here’s a visual comparison between Ridge Regression (L2), Lasso Regression (L1), and Elastic Net (L1 + L2), showing how each method constrains the coefficient estimates during regularization, as discussed above.
If you’d like to explore the full implementation, including code and data, then checkout: Github Repository 👈🏻
Stay tuned with ME, so you won’t miss out on future updates.
Until next time, happy learning!