Scaled Dot-Product Attention Explained!

Beginners Friendly In-Depth Illustrated Guide

Previously, I have covered a high-level overview about the Simple Attention Mechanism without Trainable Weights. Missed it? (really?) Go check it out.

And while you’re at it, Subscribe me so as you’ll not miss any more of these contents.

In this read, let’s gear up to improve the model by adding some trainable weights, just like those used in the original transformer architecture, the GPT models, and most other popular LLMs.

Note: This Self-Attention Mechanism is also called "Scaled Dot-Product Attention".

Here’s the overall idea (similar to before):

• Computing context vectors as weighted sums over the input vectors, specific to a certain input element.

• For this, you need attention weights (normalized attention scores that sum up to 1, using the softmax function).

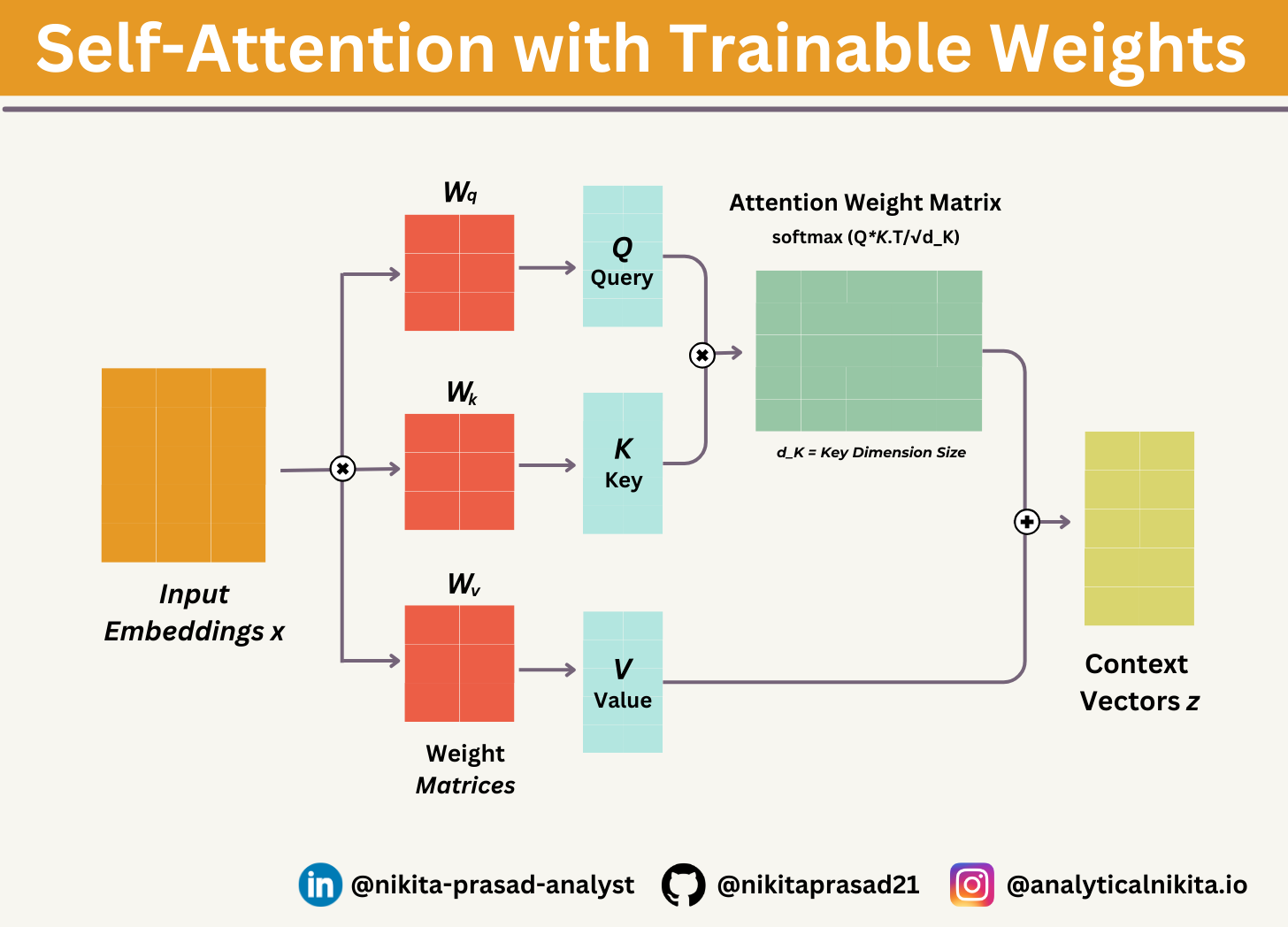
Here’s the modified architecture: 👇🏻

You can realise, there’re only slight differences compared to the basic attention mechanism, introduced earlier:

• The most notable difference is the introduction of weight matrices (W_q, W_k, and W_v) that are updated during model training.

  • These trainable weight matrices are crucial, so that the model (specifically, the attention module inside the model) can learn to produce reliable context vectors.

• Also, now you have to scale the attention scores by dividing them by the square root of the embedding dimension, √d_k (i.e., d_k**0.5):

So, that being said let’s get into the coding, and explore more!

---

Implementing Self-Attention with Trainable Weights

Let’s me start by introducing the three training weight matrices: W_q, W_k, and W_v.

These three matrices are used to project the embedded input tokens, x_i, into query, key, and value vectors via. matrix multiplication:

• Query vector: q_i =W_qx_i

• Key vector: k_i =W_kx_i

• Value vector: v_i = W_vx_i

The embedding dimensions of the input x and the query vector q can be the same or different, depending on the model's design and specific implementation.

import torch

input_emb = torch.tensor([
    [0.12, 0.45, 0.67],  # "Attention"
    [0.34, 0.56, 0.78],  # "Mechanism"
    [0.23, 0.57, 0.91],  # "drives"
    [0.76, 0.88, 0.45],  # "contextual"
    [0.54, 0.12, 0.34]   # "embedding"
], dtype=torch.float32)

Note: In GPT models, the input and output dimensions are usually the same.

But for illustration purposes, we’re using choosing different input and output dimensions to better follow the computation:

d_in = input_emb.shape[1] # the input embedding size, d=3
d_out = 2                 # the output embedding size, d=2

Following steps are implemented in the below code snippet:

Step 1: Convert Input to Query, Key, and Value Vectors: Multiply input embedding by weight matrices (Wq, Wk, Wv) to get queries (Q), keys (K), and values (V).

Step 2: Compute Attention Scores: Take the dot product of Queries and Keys to measure how much each word should focus on others.

Step 3: Scale the Scores: Divide by square root of embedding size (√dₖ) to keep values stable.

Step 4: Apply Softmax: Convert scores into probabilities so they sum to 1 (higher score = more focus).

Step 5: Compute Context Vectors: Multiply attention weights with Value vectors (V) to get the final context representation.

Step 6: Return Context Vectors: These final context vectors are returned and will be used in further layers of the GPT model.

import torch.nn as nn

class SelfAttention(nn.Module):

    def __init__(self, d_in, d_out, qkv_bias=False):
        super().__init__()
        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_key   = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)

    def forward(self, x):
        keys = self.W_key(x)
        queries = self.W_query(x)
        values = self.W_value(x)
        
        attn_scores = queries @ keys.T
        attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)

        context_vec = attn_weights @ values
        return context_vec

Note: Instead of manually defining trainable weight matrices, using PyTorch's Linear Layers (nn.Linear) has a preferred weight initialization scheme, which leads to more stable model training.

Let's instantiate a tokenizer object of SelfAttention class and tokenize our sampled input text:

torch.manual_seed(123)
sa = SelfAttention(d_in, d_out)
print(sa(input_emb))

"""
Output: 
tensor([[-0.5128, -0.0366],
        [-0.5141, -0.0376],
        [-0.5143, -0.0377],
        [-0.5143, -0.0377],
        [-0.5129, -0.0367]], grad_fn=<MmBackward0>)
"""

Bravo! You have successfully implemented a self-attention mechanism.

However, we’ve just scraped the tip of the iceberg.

Want to go deeper? Subscribe for upcoming deep dives into GPT Architectures!

If you’d like to explore the full implementation, including code and data, then checkout: Github Repository 👈🏻

---

And that’s a wrap! If you’ve made it this far — thank you so much, stay tuned with ME, so you won’t miss out on future updates.

Until next time, happy learning!

— Nikita Prasad